音声認識メモ(Kaldi)その26(パラメータ更新、NG-SGD Dan's DNN(nnet2))
パラメータ更新の過程でやっていることは「Natural Gradient for Stochastic Gradient Descent (NG-SGD)」と名前が付いている。
用語のおさらい。
「Stochastic Gradient Descent」(確率的勾配降下法)は、シャッフルした訓練データで勾配を計算、パラメータ更新を繰り返す反復法。1つの訓練データを使うのがオンライン学習、複数の訓練データを使うのがミニバッチ学習。
「Natural Gradient method」は、彼らの研究での用語で、フィッシャー情報量行列の逆行列(近似)を学習率行列として使う方法とある。
previous work has used the term “Natural Gradient” to describe methods like ours which use an approximated inverse-Fisher matrix as the learning rate matrix, so we follow their precedent in calling our method “Natural Gradient”.
コアとなる計算は、N行からなる行列Xがあったとして、i番目の行ベクトル「x_i」にフィッシャー情報量(F_i)の逆数を掛ける。

ここでのフィッシャー情報量「F_i」は、i番目の行を除く他の行「x_ j」から求める。

この考え方をベースに、以下2つの拡張を加えたとある。
- smoothing of F_i with the identity matrix (単位行列によるF_iの平滑化)
- scaling the output to have the same Frobenius norm as the input(入力と同じフロベニウスノルムを持つよう出力をスケール)
ここで、N行 x D列の行列「X_t」があるとし、「X_t」をcolumn-wise(列方向)で考えると、フィッシャー情報量行列「F_i」はD行xD列になる(X^T X)
フィッシャー情報量行列をR次元で低ランク近似して、

t : ミニバッチindex
F_t : D行 x D列
R_t : R行 x D行
D_t : R行 x R行
I : D行 x D列、identity matrix(単位行列)
rho_t : 0 < rho_t
逆行列(近似したもの)を求める。


G_t : D行 x D列
E_t : R行 x R行
beta_t : scalar
column-wise(列方向)なので、乗算は「X_t」の右側から掛けて「X_t」を更新する。

この部分は前回の以下部分にあたる。

続けてスケーリング。

この部分は前回の「gamma_t」にあたる。

細かく見てみる。
更新対象であるパラメータの次元(D)が「376」、ミニバッチサイズ(N)が「128」、低ランク近似の次元(R)が「30」であるとする。
行列X_t(N行 x D列)は、転置行列を掛けあわせて対称行列にした上で計算する。
尚、論文上では、
パラメータの次元(D) < ミニバッチの次元(N)
を想定してcolumn-wise(列方向)になっている。
(学習が進むにつれて、ミニバッチサイズは大きくなっていく(例えば「512」))
計算はD次元(=full-rank)の対称行列「T_t」(D行 x D列)に対してではなく、

S_t : D行 x D列

eta : forgetting factor、0 < η < 1
R次元(=row-rank approximation)の対称行列「Z_t」(R行 x R列)に対して行う。

Y_t : R行 x D列
R_t : R行 x D行
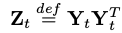
上記の「R_t」をスケールしたものを「W_t」と置き、

W_t : R行 x D行
これを重み行列として適正値に更新することがターゲットとなる。
まずは「R_t」を初期化する。
これはR次元の直交行列を横に並べた形になる。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::InitDefault()
// after the next line, W_t_ will store the orthogonal matrix R_t. InitOrthonormalSpecial(&W_t_);
R_t (R x D)

「E_t」の初期値を求め、その0.5乗(平方根)を掛ける。
BaseFloat E_tii = 1.0 / ( 2.0 + (D + rank_) * alpha_ / D );
// W_t =(def) E_t^{0.5} R_t.
W_t_.Scale(sqrt(E_tii));次のミニバッチに向けて「W_t」を更新する。
更新式は以下のとおり。

W_t1 : R行 x D列
E_t1 : R行 x R行、diagonal matrix(対角行列)
R_t1 : R行 x D列
C_t : R行 x R行、diagonal matrix(対角行列)
U_t : R行 x R列、Orthogonal matrix(直交行列)
Y_t : R行 x D列
J_t : R行 x D列
D_t : R行 x R行
eta : forgetting factor、0 < η < 1
「U_t」(直交行列)と「C_t」(特異値)は、「Z_t」を特異値分解して得られる。

以下、「Z_t」を求める過程。
元々のインプット「X_t」(N行 x D列)に、「W_t」(R行 x D列)の転置行列を右から掛けて、「H_t」(N行 x R列)を求める(「N」はミニバッチサイズ)
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
H_t.AddMatMat(1.0, *X_t, kNoTrans, W_t, kTrans, 0.0); // H_t = X_t W_t^T
H_t (N x R)

列数「D」(376次元)のインプット(X_t)が、列数「R」(30次元)の行列になる。
続けて、「J_t」を求める。
元々のインプット「X_t」(N行 x D列)に「H_t」(N行 x R列)の転置行列を左から掛け合わせて「J_t」(R行 x D列)を求める。
(「W_t」と同じ行数、列数になる)
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
J_t.AddMatMat(1.0, H_t, kTrans, *X_t, kNoTrans, 0.0); // J_t = H_t^T X_t
「J_t」を式変形すると
J_t = H_t^T X_t
= (X_t W_t^T)^T X_t
= W_t X_t^T X_t「X_t」(N行 x D列)の「uncentered covariance matrix」(D行 x D列)に、Weight Matrix(R行 x D列)を左から掛けたものとも言える。
J_t (R x D)

続けて「K_t」を求める。
「J_t」(R行 x D列)に対し、転置行列を右から掛けたものにあたる。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
K_t.SymAddMat2(1.0, J_t, kNoTrans, 0.0); // K_t = J_t J_t^T
K_t (R x R、symmetric)

続けて「L_t」を求める。
「H_t」(N行 x R列)に対し、転置行列を左から掛けたものにあたる。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
L_t.SymAddMat2(1.0, H_t, kTrans, 0.0); // L_t = H_t^T H_t
L_t (R x R、symmetric)

「K_t」と「L_t」を使って、「Z_t」を求める。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
SpMatrix<double> Z_t_double(R); ComputeZt(N, rho_t, d_t, inv_sqrt_e_t, K_t_cpu, L_t_cpu, &Z_t_double);
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
Matrix<BaseFloat> U_t(R, R); Vector<BaseFloat> c_t(R); // do the symmetric eigenvalue decomposition Z_t = U_t C_t U_t^T. Z_t_scaled.Eig(&c_t, &U_t); SortSvd(&c_t, &U_t); c_t.Scale(z_t_scale);
C_t (30次元)
0.957 0.164 0.119 0.090 ... 0.00019 0.00016
U_t (R x R)

「W_t」を更新する。

[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
CuMatrix<BaseFloat> W_t1(R, D); // W_{t+1}
ComputeWt1(N,
d_t,
d_t1,
rho_t,
rho_t1,
U_t,
sqrt_c_t,
inv_sqrt_e_t,
W_t,
&J_t,
&W_t1);「B_t」を求める。
B_t (R x D)

[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::ComputeWt1()
// B_t = J_t + (1-eta)/(eta/N) (D_t + rho_t I) W_t J_t->AddDiagVecMat(1.0, w_t_coeff_gpu, W_t, kNoTrans, 1.0);
w_t_coeff_gpu : R行 x R行、対角行列、W_tの各行に対する係数
式変形すると以下のとおり。
B_t = J_t + ( W_t係数 * W_t )
= ( W_t X_t^T X_t ) + ( W_t係数 * W_t )「A_t」を求める。
A_t (R x R)

[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::ComputeWt1()
// A_t = (eta/N) E_{t+1}^{0.5} C_t^{-0.5} U_t^T E_t^{-0.5} B_t
Matrix<BaseFloat> A_t(U_t, kTrans);
for (int32 i = 0; i < R; i++) {
BaseFloat i_factor = (eta / N) * sqrt_e_t1(i) * inv_sqrt_c_t(i);
for (int32 j = 0; j < R; j++) {
BaseFloat j_factor = inv_sqrt_e_t(j);
A_t(i, j) *= i_factor * j_factor;
}
}「W_t1」を求める。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::ComputeWt1()
// W_{t+1} = A_t B_t
CuMatrix<BaseFloat> A_t_gpu(A_t);
W_t1->AddMatMat(1.0, A_t_gpu, kNoTrans, *J_t, kNoTrans, 0.0);「W_t1」を使って「X_t」を更新する。

これを繰り返して、更新された「X_t」が、前回見た「in_value_temp」、「out_deriv_temp」に該当する。
[ nnet2/nnet-component.cc ] AffineComponentPreconditionedOnline::Update()
preconditioner_in_.PreconditionDirections(&in_value_temp,
&in_row_products,
&in_scale);
preconditioner_out_.PreconditionDirections(&out_deriv_temp,
&out_row_products,
&out_scale);パラメータの修正ベクトルとして使い、モデルのパラメータを更新。
[ nnet2/nnet-component.cc ] AffineComponentPreconditionedOnline::Update()
bias_params_.AddMatVec(local_lrate, out_deriv_temp, kTrans, precon_ones, 1.0); linear_params_.AddMatMat(local_lrate, out_deriv_temp, kTrans, in_value_precon_part, kNoTrans, 1.0);
