パラメータ推定（混合正規分布）

混合分布を使うことで、より柔軟に分布をモデル化できる。

例えば、ピークが2つあるような分布。
f:id:ichou1:20181028085746p:plain

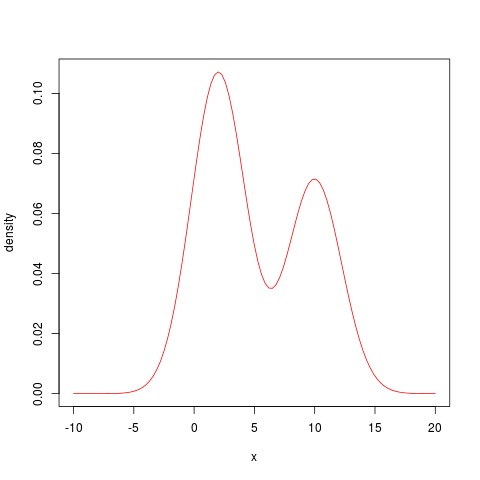
これは以下２つの分布を混合したもの。
分布1 : 正規分布N(2, 5)、混合比「0.6」
分布2 : 正規分布N(10, 5)、混合比「0.4」

この混合分布は音声認識において使われていて、隠れマルコフモデル（HMM）の各状態の出力確率が混合正規分布（混合ガウス分布）に従うとしたモデルを「GMM-HMM」と呼ぶ。

具体的にどのようにモデル化しているかは以下の記事に書いた。
work-in-progress.hatenablog.com

今回は混合正規分布の最尤推定に関するメモ。

混合数をKとおく。

混合パラメータ

$\begin{eqnarray} \displaystyle \sum_{ k = 1 }^K \pi_k &=& 1 \quad \left( 0 \leq \pi_k \leq 1 \right) \end{eqnarray}$

混合正規分布の確率密度関数

$\begin{eqnarray} p(x \ | \ \pi_k, \mu_k, \sigma_k^2 ) &=& \displaystyle \sum_{ k = 1 }^K \pi_k \ \ f(x \ | \ \mu_k, \sigma_k^2 ) \end{eqnarray}$

$\begin{eqnarray} f(x \ | \ \mu, \sigma^2 ) &=& \frac{1}{\sqrt{2\pi\sigma^{2}}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2} \right) \end{eqnarray}$

観測データがN個のときの対数尤度関数

$\begin{eqnarray} l(\pi_k, \mu_k, \sigma_k^2 ) &=& \log L(\pi_k, \mu_k, \sigma_k^2 ) \\ &=& \log \displaystyle \prod_{ n = 1 }^N p(x_n \ | \ \pi_k, \mu_k, \sigma_k^2 ) \\ &=& \displaystyle \sum_{ n = 1 }^N \log p(x_n \ | \ \pi_k, \mu_k, \sigma_k^2 ) \\ &=& \displaystyle \sum_{ n = 1 }^N \log \left( \displaystyle \sum_{ k = 1 }^K \pi_k \ f(x_n \ | \ \mu_k, \sigma_k^2 ) \right) \end{eqnarray}$

xが与えられたとき、それに対応する確率密度を各分布ごとに分解した割合を仮置きするために、潜在変数zを導入する。
潜在変数zは、K個の要素からなり、どれか1つだけ1を取り、他は全て0となる。
xについてn番目の値が与えられたとき、k番目のｚが1となる確率を負担率と呼び、以下の式で計算する。

$\begin{eqnarray} \gamma(z_{nk}) &=& P(z_k =1 | x_n) \\ \\ &=& \frac{\pi_k N(x_n|\mu_k, \sigma_k^2)}{\displaystyle \sum_{k=1}^K \pi_k N(x_n|\mu_k, \sigma_k^2)} \end{eqnarray}$

分母は、混合分布における、n番目のxの確率密度。
分子は、k番目の分布における、n番目のxの確率密度となるので、負担率は

$0 \leq \gamma(z_{nk}) \leq 1 \\ \begin{eqnarray} \displaystyle \sum_{k=1}^K \gamma(z_{nk}) &=& 1 \end{eqnarray}$

この辺は以下のサイトを参考にさせていただいた。
混合ガウスモデルとEM - 人工知能に関する断創録

負担率はN個のxのそれぞれについて求まる。
この負担率を使って、パラメータ（平均、分散、混合比）の最尤値を計算する。

$\begin{eqnarray} \mu_{k \ new} &=& \frac{ \displaystyle \sum_{ n = 1 }^N \left( \ \gamma(z_{nk}) \ x_n \ \right) }{ \displaystyle \sum_{ n = 1 }^N \gamma(z_{nk}) } \\ \\ \sigma_{k \ new}^2 &=& \frac{ \displaystyle \sum_{ n = 1 }^N \left( \ \gamma(z_{nk}) \ (x_n -\mu_k)^2 \ \right) }{\displaystyle \sum_{ n = 1 }^N \gamma(z_{nk}) } \\ \\ \pi_{k \ new} &=& \frac{\displaystyle \sum_{ n = 1 }^N \gamma(z_{nk}) }{ \displaystyle \sum_{ k = 1 }^K \displaystyle \sum_{ n = 1 }^N \gamma(z_{nk}) } \end{eqnarray}$

負担率を求めるためにはパラメータが必要で、パラメータの最尤値を計算するためには負担率が必要と、循環してしまうので、以下の2ステップに分けて計算する。

Eステップ：現在の混合比、平均、分散に対応する負担率を計算する
Mステップ：Eステップで計算した負担率をもとに、混合比、平均、分散の最尤値を求める

混合ガウス分布の数が「2」、各分布が以下であるサンプルデータ「500」個用意し、推定の過程を追ってみる。
分布1 : 正規分布、平均「2」、分散「5」、混合比「0.6」
分布2 : 正規分布、平均「10」、分散「5」、混合比「0.4」

rnorm関数に与えるseedは「123」を指定。

 [1]  0.7467384  1.4853075  5.4853777  2.1576616  2.2890962  9.7872438
 [7]  3.0306400 -0.8287629  0.4641503  1.0034695  9.7822757  2.8045682
[13]  2.8961522 10.4597300  8.6216076  5.9956592  9.7052800 -2.3974896
(snip)
[486]  3.741583972  4.045495218 11.760084269  5.637816986 13.701085639
[491] 11.511050698  5.139551842  4.893659583  9.523030728 10.700400827
[496]  9.798809343 12.393746629  2.368595386  8.831393539  3.234662183

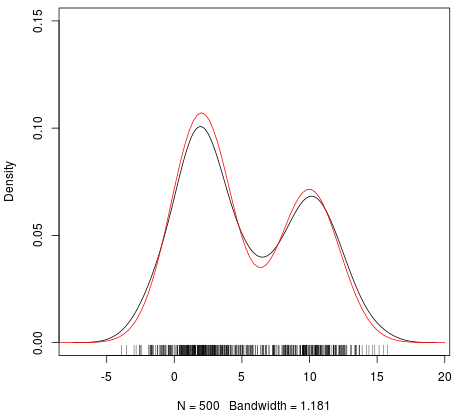
密度プロット（赤い線はcurve関数で書いた真の確率密度関数）
f:id:ichou1:20181030194850p:plain

「R」には「mixtool」ライブラリで「normalmixEM」関数が用意されているので、これを使えば最尤値を求められる。

検算の意味で最初に値を求めておく。

mixtool_val <- normalmixEM(data, k=2)

最尤値での対数尤度

mixtool_val$all.loglik[length(mixtool_val$all.loglik)]
-1388.84

最尤値（混合比、平均、分散）

mixtool_val$lambda
[1] 0.589741 0.410259    # 混合比 

mixtool_val$mu
[1]  1.969816 10.129432  # 平均

mixtool_val$sigma^2
[1] 4.498699 4.566088    # 分散

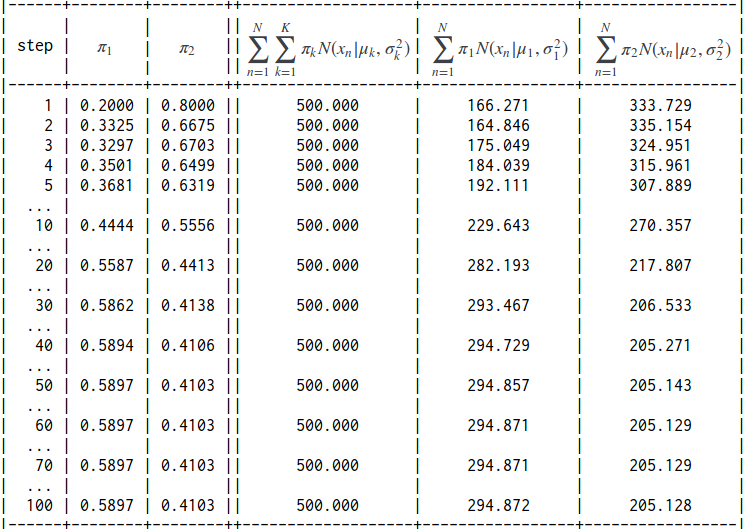
先ほどの式で最尤値を100回、計算してみた結果。
初期値は、以下の値を与えた。
分布1 : 混合比0.2、平均1、分散2
分布2 : 混合比0.8、平均5、分散2

f:id:ichou1:20181031163918p:plain

負担率の推移。
f:id:ichou1:20181031163929p:plain

ichou1のブログ

主に音声認識、時々、データ分析のことを書く