音声認識メモ(Kaldi)その26(パラメータ更新、NG-SGD Dan's DNN(nnet2))
パラメータ更新の過程でやっていることは「Natural Gradient for Stochastic Gradient Descent (NG-SGD)」と名前が付いている。
用語のおさらい。
「Stochastic Gradient Descent」(確率的勾配降下法)は、シャッフルした訓練データで勾配を計算、パラメータ更新を繰り返す反復法。1つの訓練データを使うのがオンライン学習、複数の訓練データを使うのがミニバッチ学習。
「Natural Gradient method」は、彼らの研究での用語で、フィッシャー情報量行列の逆行列(近似)を学習率行列として使う方法とある。
previous work has used the term “Natural Gradient” to describe methods like ours which use an approximated inverse-Fisher matrix as the learning rate matrix, so we follow their precedent in calling our method “Natural Gradient”.
コアとなる計算は、N行からなる行列Xがあったとして、i番目の行ベクトル「x_i」にフィッシャー情報量(F_i)の逆数を掛ける。

ここでのフィッシャー情報量「F_i」は、i番目の行を除く他の行「x_ j」から求める。

この考え方をベースに、以下2つの拡張を加えたとある。
- smoothing of F_i with the identity matrix (単位行列によるF_iの平滑化)
- scaling the output to have the same Frobenius norm as the input(入力と同じフロベニウスノルムを持つよう出力をスケール)
ここで、N行 x D列の行列「X_t」があるとし、「X_t」をcolumn-wise(列方向)で考えると、フィッシャー情報量行列「F_i」はD行xD列になる(X^T X)
フィッシャー情報量行列をR次元で低ランク近似して、

t : ミニバッチindex
F_t : D行 x D列
R_t : R行 x D行
D_t : R行 x R行
I : D行 x D列、identity matrix(単位行列)
rho_t : 0 < rho_t
逆行列(近似したもの)を求める。


G_t : D行 x D列
E_t : R行 x R行
beta_t : scalar
column-wise(列方向)なので、乗算は「X_t」の右側から掛けて「X_t」を更新する。

この部分は前回の以下部分にあたる。

続けてスケーリング。

この部分は前回の「gamma_t」にあたる。

細かく見てみる。
更新対象であるパラメータの次元(D)が「376」、ミニバッチサイズ(N)が「128」、低ランク近似の次元(R)が「30」であるとする。
行列X_t(N行 x D列)は、転置行列を掛けあわせて対称行列にした上で計算する。
尚、論文上では、
パラメータの次元(D) < ミニバッチの次元(N)
を想定してcolumn-wise(列方向)になっている。
(学習が進むにつれて、ミニバッチサイズは大きくなっていく(例えば「512」))
計算はD次元(=full-rank)の対称行列「T_t」(D行 x D列)に対してではなく、

S_t : D行 x D列

eta : forgetting factor、0 < η < 1
R次元(=row-rank approximation)の対称行列「Z_t」(R行 x R列)に対して行う。

Y_t : R行 x D列
R_t : R行 x D行
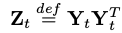
上記の「R_t」をスケールしたものを「W_t」と置き、

W_t : R行 x D行
これを重み行列として適正値に更新することがターゲットとなる。
まずは「R_t」を初期化する。
これはR次元の直交行列を横に並べた形になる。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::InitDefault()
// after the next line, W_t_ will store the orthogonal matrix R_t. InitOrthonormalSpecial(&W_t_);
R_t (R x D)

「E_t」の初期値を求め、その0.5乗(平方根)を掛ける。
BaseFloat E_tii = 1.0 / ( 2.0 + (D + rank_) * alpha_ / D );
// W_t =(def) E_t^{0.5} R_t.
W_t_.Scale(sqrt(E_tii));次のミニバッチに向けて「W_t」を更新する。
更新式は以下のとおり。

W_t1 : R行 x D列
E_t1 : R行 x R行、diagonal matrix(対角行列)
R_t1 : R行 x D列
C_t : R行 x R行、diagonal matrix(対角行列)
U_t : R行 x R列、Orthogonal matrix(直交行列)
Y_t : R行 x D列
J_t : R行 x D列
D_t : R行 x R行
eta : forgetting factor、0 < η < 1
「U_t」(直交行列)と「C_t」(特異値)は、「Z_t」を特異値分解して得られる。

以下、「Z_t」を求める過程。
元々のインプット「X_t」(N行 x D列)に、「W_t」(R行 x D列)の転置行列を右から掛けて、「H_t」(N行 x R列)を求める(「N」はミニバッチサイズ)
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
H_t.AddMatMat(1.0, *X_t, kNoTrans, W_t, kTrans, 0.0); // H_t = X_t W_t^T
H_t (N x R)

列数「D」(376次元)のインプット(X_t)が、列数「R」(30次元)の行列になる。
続けて、「J_t」を求める。
元々のインプット「X_t」(N行 x D列)に「H_t」(N行 x R列)の転置行列を左から掛け合わせて「J_t」(R行 x D列)を求める。
(「W_t」と同じ行数、列数になる)
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
J_t.AddMatMat(1.0, H_t, kTrans, *X_t, kNoTrans, 0.0); // J_t = H_t^T X_t
「J_t」を式変形すると
J_t = H_t^T X_t
= (X_t W_t^T)^T X_t
= W_t X_t^T X_t「X_t」(N行 x D列)の「uncentered covariance matrix」(D行 x D列)に、Weight Matrix(R行 x D列)を左から掛けたものとも言える。
J_t (R x D)

続けて「K_t」を求める。
「J_t」(R行 x D列)に対し、転置行列を右から掛けたものにあたる。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
K_t.SymAddMat2(1.0, J_t, kNoTrans, 0.0); // K_t = J_t J_t^T
K_t (R x R、symmetric)

続けて「L_t」を求める。
「H_t」(N行 x R列)に対し、転置行列を左から掛けたものにあたる。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
L_t.SymAddMat2(1.0, H_t, kTrans, 0.0); // L_t = H_t^T H_t
L_t (R x R、symmetric)

「K_t」と「L_t」を使って、「Z_t」を求める。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
SpMatrix<double> Z_t_double(R); ComputeZt(N, rho_t, d_t, inv_sqrt_e_t, K_t_cpu, L_t_cpu, &Z_t_double);
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
Matrix<BaseFloat> U_t(R, R); Vector<BaseFloat> c_t(R); // do the symmetric eigenvalue decomposition Z_t = U_t C_t U_t^T. Z_t_scaled.Eig(&c_t, &U_t); SortSvd(&c_t, &U_t); c_t.Scale(z_t_scale);
C_t (30次元)
0.957 0.164 0.119 0.090 ... 0.00019 0.00016
U_t (R x R)

「W_t」を更新する。

[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
CuMatrix<BaseFloat> W_t1(R, D); // W_{t+1}
ComputeWt1(N,
d_t,
d_t1,
rho_t,
rho_t1,
U_t,
sqrt_c_t,
inv_sqrt_e_t,
W_t,
&J_t,
&W_t1);「B_t」を求める。
B_t (R x D)

[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::ComputeWt1()
// B_t = J_t + (1-eta)/(eta/N) (D_t + rho_t I) W_t J_t->AddDiagVecMat(1.0, w_t_coeff_gpu, W_t, kNoTrans, 1.0);
w_t_coeff_gpu : R行 x R行、対角行列、W_tの各行に対する係数
式変形すると以下のとおり。
B_t = J_t + ( W_t係数 * W_t )
= ( W_t X_t^T X_t ) + ( W_t係数 * W_t )「A_t」を求める。
A_t (R x R)

[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::ComputeWt1()
// A_t = (eta/N) E_{t+1}^{0.5} C_t^{-0.5} U_t^T E_t^{-0.5} B_t
Matrix<BaseFloat> A_t(U_t, kTrans);
for (int32 i = 0; i < R; i++) {
BaseFloat i_factor = (eta / N) * sqrt_e_t1(i) * inv_sqrt_c_t(i);
for (int32 j = 0; j < R; j++) {
BaseFloat j_factor = inv_sqrt_e_t(j);
A_t(i, j) *= i_factor * j_factor;
}
}「W_t1」を求める。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::ComputeWt1()
// W_{t+1} = A_t B_t
CuMatrix<BaseFloat> A_t_gpu(A_t);
W_t1->AddMatMat(1.0, A_t_gpu, kNoTrans, *J_t, kNoTrans, 0.0);「W_t1」を使って「X_t」を更新する。

これを繰り返して、更新された「X_t」が、前回見た「in_value_temp」、「out_deriv_temp」に該当する。
[ nnet2/nnet-component.cc ] AffineComponentPreconditionedOnline::Update()
preconditioner_in_.PreconditionDirections(&in_value_temp,
&in_row_products,
&in_scale);
preconditioner_out_.PreconditionDirections(&out_deriv_temp,
&out_row_products,
&out_scale);パラメータの修正ベクトルとして使い、モデルのパラメータを更新。
[ nnet2/nnet-component.cc ] AffineComponentPreconditionedOnline::Update()
bias_params_.AddMatVec(local_lrate, out_deriv_temp, kTrans, precon_ones, 1.0); linear_params_.AddMatMat(local_lrate, out_deriv_temp, kTrans, in_value_precon_part, kNoTrans, 1.0);
固有値分解と座標変換
DNN(Deep Neural Network)を学んでいると、擬似逆行列の算出や低ランク近似などで固有値の概念に出くわす。
固有値分解に関するメモ。
以下のサイトを参考にさせていただいた。
http://eman-physics.net/math/linear09.html
変換に使う行列Aは参考サイトと同じもの使用。
固有値
D <- diag(A.eigen$values) [,1] [,2] [1,] 5 0 [2,] 0 2
固有ベクトル
# 固有値5に属する固有ベクトル(正規化)) U1 <- A.eigen$vectors[,1] [1] -0.4472136 -0.8944272 # 固有値2に属する固有ベクトル(正規化)) U2 <- A.eigen$vectors[,2] [1] -0.7071068 0.7071068
2つのベクトルの内積は非ゼロなので、
# 2つの固有ベクトルの内積 U1 %*% U2 [,1] [1,] -0.3162278
2つの固有ベクトル( -0.45, -0.89 )、 ( -0.71, 0.71 )は直交しない。
視覚化してみる。
適当な4つの点P1( 1, 2 )、P2( 1, 1 )、P3( 1, 0 )、P4( -1, -2 )を選ぶ。
P1 <- matrix(c(1, 2), nrow=2, ncol=1, byrow=FALSE) P2 <- matrix(c(1, 1), nrow=2, ncol=1, byrow=FALSE) P3 <- matrix(c(1, 0), nrow=2, ncol=1, byrow=FALSE) P4 <- matrix(c(-1, -2), nrow=2, ncol=1, byrow=FALSE)

1次変換によって移される座標を求める。
P1の1次変換
A %*% P1 [,1] [1,] 5 [2,] 10
(1, 2)から(5, 10)へ移った。
P2の1次変換
A %*% P2 [,1] [1,] 4 [2,] 6
(1, 1)から(4, 6)へ移った。
P3の1次変換
A %*% P3 [,1] [1,] 3 [2,] 2
(1, 0)から(3, 2)へ移った。
P4の1次変換
A %*% P4 [,1] [1,] -5 [2,] -10
(-1, -2)から(-5, -10)へ移った。
変換前と変換後の座標をプロットしてみる。
白抜きが元の座標、同じ形の黒塗りが1次変換によって移された座標を示す。

ここでは、P1とP4が該当。
P1に関しては(1, 2)だったものが(5, 10)に移っており、5倍(固有値と同じ)されている。
また、P4に関しては(-1, -2)だったものが(-5, -10)に移っており、同じく5倍(固有値と同じ)されている。
固有ベクトルを基底とする新しい座標軸で、各点がどう表現されるか確認。
固有ベクトルを列ベクトルとして表し、横に並べた行列
V <- A.eigen$vectors [,1] [,2] [1,] -0.4472136 -0.7071068 [2,] -0.8944272 0.7071068
この逆行列を、元の座標を表す列ベクトルの左から掛けることで、新しい基底での座標が求まる。
何故こんなことをするのかは、無相関化の項をご参照。
work-in-progress.hatenablog.com
P1の新座標表現
solve(V) %*% P1 [,1] [1,] -2.236068e+00 [2,] 2.220446e-16
小数点第二位を四捨五入すると(-2.24, 0)
P2の新座標表現
solve(V) %*% P2 [,1] [1,] -1.4907120 [2,] -0.4714045
小数点第二位を四捨五入すると(-1.49, -0.47)
P3の新座標表現
solve(V) %*% P3 [,1] [1,] -0.745356 [2,] -0.942809
小数点第二位を四捨五入すると(-0.75, -0.94)
P4の新座標表現
solve(V) %*% P4 [,1] [1,] 2.236068e+00 [2,] -2.220446e-16
小数点第二位を四捨五入すると(2.24, 0)
プロットしてみる。
元々の基底(1, 0)、(0, 1)は消して、新しい基底(-0.45, -0.89)、 (-0.71, 0.71)を描画。
枠外の目盛りは元々の基底(1, 0)、(0, 1)のもの。目印として残した。

拡大。

座標軸の正負の向きが標準基底と同じになるよう、回転および反転。

再掲
P1(-2.24, 0) <== 標準基底での表現(1, 2)
P2(-1.49, -0.47) <==標準基底での表現(1, 1)
P3(-0.75, -0.94) <==標準基底での表現(1, 0)
P4(2.24, 0) <==標準基底での表現(-1, -2)
R 計算メモ(行列を使った分散、共分散の計算)
行列計算で分散、共分散を求める方法のメモ。
前回使った2変数データ(xとy、サンプル数5)を以下のとおり行列で表現する。
(各変数は、列ベクトルでなく、行ベクトルで表現していることに注意)

元データ
# 変数x xvar [1] 50 60 70 80 90 # 変数y yvar [1] 40 70 90 60 100
センタリングする(偏差に置き換える)

この行列をAと置く。
行列表現(センタリング後)
A <- matrix(c(scale(xvar, scale=F), scale(yvar, scale=F)), nrow=2, ncol=5, byrow=TRUE) [,1] [,2] [,3] [,4] [,5] [1,] -20 -10 0 10 20 [2,] -32 -2 18 -12 28
以下の計算により(標本)分散共分散行列が求まる。
標本分散共分散行列(各変数が行データとして表現される場合)
Nはサンプル数、Tは転置行列を表す
行列計算(標本分散共分散行列を求める、行ベクトル表現)
(1 / ncol(A) ) * ( A %*% t(A)) [,1] [,2] [1,] 200 220 [2,] 220 456
N-1で割れば、不偏分散共分散行列が求まる。
行列計算(不偏分散共分散行列を求める)
(1 / (ncol(A)-1) ) * ( A %*% t(A)) [,1] [,2] [1,] 250 275 [2,] 275 570
ある論文を見ていると、「uncentered covariance matrix」という言葉が出てきた。
センタリングしないで求めた分散共分散行列のようだが、その性質を確認してみる。
センタリングしない行列をBとおく。
行列表現(センタリング無し)
[,1] [,2] [,3] [,4] [,5] [1,] 50 60 70 80 90 [2,] 40 70 90 60 100
行列計算(標本分散共分散行列を求める)
obs_cov <- (1 / ncol(B)) * ( B %*% t(B)) [,1] [,2] [1,] 5100 5260 [2,] 5260 5640
このデータを使って標本分散を求める。
# xの標本分散 obs_cov[1,][1] - mean(xvar)^2 [1] 200 # yの標本分散 obs_cov[2,][2] - mean(yvar)^2 [1] 456
センタリングしたもの、しないものとで、xの標本分散、yの標本分散、xyの共分散の大小関係は保たれる模様だし、分散の大小関係が分かれば良いようなケースで使うものだろうか。
尚、各変数を列ベクトルで表現する場合、行列計算は以下のとおりとなる。
標本分散共分散行列(各変数が列データとして表現される場合)
行列表現(センタリング後)
A <- matrix(c(scale(xvar, scale=F), scale(yvar, scale=F)), nrow=5, ncol=2, byrow=FALSE) [,1] [,2] [1,] -20 -32 [2,] -10 -2 [3,] 0 18 [4,] 10 -12 [5,] 20 28
行列計算(標本分散共分散行列を求める、列ベクトル表現)
(1 / nrow(A)) * ( t(A) %*% A) [,1] [,2] [1,] 200 220 [2,] 220 456
R 計算メモ(分散、共分散)
分散と共分散を計算をしたいとき用のメモ。
Rでは、標本分散、標本共分散を求める関数はないので、自分で定義する。
以下のサイトを参考にさせていただいた。
http://cse.naro.affrc.go.jp/takezawa/r-tips/r/59.html
関数定義ここから。
標本分散
# 関数を定義(標本分散) variance <- function(x) { var(x) * (length(x)-1) / length(x) }
標本共分散
# 関数を定義(2変数の標本共分散) # 2変数(xとy)の不偏共分散 : var(x, y) covariance <- function(x, y) { var(x, y) * (length(x)-1)/length(x) }
標本標準偏差
# 関数を定義(標本標準偏差) stddev <- function(x) { sqrt(variance(x)) }
相関係数
# 関数を定義(標本分散と標本共分散を使った相関係数) # cor(x, y)と同じになる correlation <- function(x, y) { covariance(x, y) / (stddev(x) * stddev(y)) }
検算。以下のサイトのデータを使わせいただいた。
https://sci-pursuit.com/math/statistics/correlation-coefficient.html
元データ(2変数、xとy)
# 変数x (英語の点数) xvar <- c(50, 60, 70, 80, 90) # 変数y (数学の点数) yvar <- c(40, 70, 90, 60, 100)
分散
# 変数xの標本分散 variance(xvar) [1] 200 # (参考)変数xの不偏分散 var(xvar) [1] 250 # 変数yの標本分散 variance(yvar) [1] 456 # (参考)変数yの不偏分散 var(yvar) [1] 570
標準偏差
# 変数xの標本標準偏差 stddev(xvar) [1] 14.14214 # (参考)変数xの不偏標準偏差 sd(xvar) [1] 15.81139 # 変数yの標本標準偏差 stddev(yvar) [1] 21.35416 # (参考)変数yの不偏標準偏差 sd(yvar) [1] 23.87467
共分散
# 2変数の標本共分散 covariance(xvar, yvar) [1] 220 # (参考)2変数の不偏共分散 cov(xvar, yvar) [1] 275
相関係数
# 2変数の相関係数(標本分散、標本共分散を使うパターン) correlation(xvar, yvar) [1] 0.7284928 # (参考)2変数の相関係数 (R標準の関数) > cor(xvar, yvar) [1] 0.7284928
相関係数は不偏、標本のどちらを使っても同じ結果になる。
計算式の分母(割る数)は、標本の方が大きいので(標本はN、不偏はN-1)、大小関係は以下のとおりとなる。
グラフ化
ggplot2を使って、2変数を散布図にプロットする方法。
library(ggplot2) obs <- data.frame(x=xvar, y=yvar) g <- ggplot(obs, aes(x=xvar, y=yvar)) g <- g + xlim(0, 100) + ylim(0, 100) g <- g + geom_point() plot(g)

音声認識メモ(Kaldi)その25(内部で扱うデータの型)
プログラム内で扱うデータの桁数に関するメモ。
デフォルトでコンパイルすると「float」型になる。
kaldi/configure at master · kaldi-asr/kaldi · GitHub
configure抜粋
# Default configuration double_precision=false (snip) if $double_precision; then echo "DOUBLE_PRECISION = 1" >> kaldi.mk else echo "DOUBLE_PRECISION = 0" >> kaldi.mk fi
DOUBLE_PRECISIONが「0」なら、テンプレート部分はfloat型でコンパイルされる。
matrix/kaldi-matrix.cc
template<typename Real>
void Matrix<Real>::Read(std::istream & is, bool binary, bool add) {
Real r;
is >> r;マシンにdouble型を扱う回路が付いているなら、double型にした方が速くなるのかもしれない。
以下はデータ読み込みに関するメモ。
以下のような指数表記で書かれたテキストファイルがあったとして、
-6.93889018e-18 -5.55112e-17 ...
以下のコードでちゃんと読んでくれる。
float r; is >> r;
音声認識メモ(Kaldi)その24( パラメータ更新 Dan's DNN(nnet2))
「AffineComponentPreconditionedOnline」コンポーネントのパラメータ更新過程を追ってみる。
モデルは「nnet4c」ベース、mixupを行う前の状態。

今回、確認するのは下図の破線部分のパラメータ。

BackPropagationにおいて、以下2つの値を使って更新する。
尚、ここでのminibatch-sizeは「128」であるとする。
- 「in_value_temp」 : PropagationでTanhコンポーネントを通した後の値(128row x 375col)に対して、各行の最後に「1.0」を加えたもの(128row x 376col)
- 「out_deriv_temp」 : BackpropagationでSoftmaxコンポーネントを通した後の値のコピー(128row x 192col)
AffineComponentPreconditionedOnlineクラスのメンバである2つのOnlinePreconditionerクラスに上記2つをそれぞれ渡す。
nnet2/nnet-component.cc
void AffineComponentPreconditionedOnline::Update(
CuMatrixBase<BaseFloat> &in_value,
const CuMatrixBase<BaseFloat> &out_deriv)
{
...
preconditioner_in_.PreconditionDirections(&in_value_temp,
&in_row_products,
&in_scale);
preconditioner_out_.PreconditionDirections(&out_deriv_temp,
&out_row_products,
&out_scale);
...ここでの処理内容の詳細はDan氏の論文に書かれている。
更新前のin_value_temp(128row x 376col、 論文中の「X_t」に該当
0.265 0.362 -0.999 -0.999 -0.946 ... 1 ...
t : minibatch index
ここから、X_hat_tを求める。

R=30(rankIn(低ランク近似)の次元)
「W_t」はR x DのWeight Matrix(D=376)
N=128(minibatch size)
更新後のin_value_temp(128row x 376col、 論文中の「X_hat_t」に該当
0.035 0.562 -0.010 0.040 -0.575 ... ...
該当するソースコード箇所(nnet-precondition-online.cc)
// X_hat_t = X_t - H_t W_t X_t->AddMatMat(-1.0, H_t, kNoTrans, W_t, kNoTrans, 1.0);
「X_hat_t」の各行の内積( (0.035 * 0.035) + (0.562 * 0.562) + (-0.010 * -0.010) + ...)を求める。
これが「in_row_products」に該当する。
in_row_products (128dim)
62.02 44.57 66.93 81.97 59.58 ...
また、以下の式により、gamma_tを求める。
これが「in_scale」に該当する。

in_scale
2.04739451
「preconditioner_out_」に対しても同様の処理を行う。
更新前のout_deriv_temp(128row x 192col、論文中の「X_t」に該当)
-0.000 -6.5e-06, -9.9e-06, -1.2-06, -7.5e-07 ... ...
更新後のout_deriv_temp(128row x 192col、論文中の「X_hat_t」に該当)
0.048 -5.5e-06 -0.000 5.9e-08 -0.000 ... ...
out_row_products(128dim)
0.136 0.163 0.000 0.072 0.008 ...
out_scale
2.1778152
「in_value_temp」(128row x 376dim)より、「in_value_precon_part」(128row x 375dim)、「precon_ones」(128dim)を求める。
AffineComponentPreconditionedOnline::Update()の内部処理
CuSubMatrix<BaseFloat> in_value_precon_part(in_value_temp,
0, in_value_temp.NumRows(),
0, in_value_temp.NumCols() - 1);
CuVector<BaseFloat> precon_ones(in_value_temp.NumRows());
precon_ones.CopyColFromMat(in_value_temp, in_value_temp.NumCols() - 1);「in_scale」、「out_scale」、「in_row_products」、「out_row_products」より、当該ミニバッチの「scale」および「minibatch_scale」を求める。
以上のデータをもとに、パラメータを更新する。
AffineComponentPreconditionedOnline::Update()の内部処理
BaseFloat local_lrate = scale * minibatch_scale * learning_rate_;
bias_params_.AddMatVec(local_lrate, out_deriv_temp, kTrans,
precon_ones, 1.0);
linear_params_.AddMatMat(local_lrate, out_deriv_temp, kTrans,
in_value_precon_part, kNoTrans, 1.0);
OpenSSL APIメモ(HTTP/2対応その1)
OpenSSL APIを使うクライアントプログラムで「SSL_ERROR_SYSCALL」が返ってきた。
エラーを返している部分はSSL_connect()
通信内容を確認してみると、アクセスしようとしているサイトはHTTP/2対応だった。
(WEBサーバはNginx)
段階的に修正してみる。
HTTP/2ではTLS1.2以降を使う必要があるようなので、
SSL_CTX_new(TLSv1_client_method());
を以下のように変更する。
SSL_CTX_new(TLSv1_2_client_method());
SSL_connect()は通ったがレスポンスは以下のとおり。
Status :505 Method :HTTP/1.1
HTTP2でネゴシエーションするためにはどうするか。
ALPNと呼ばれるTLS拡張を使う模様。
1.0.2から対応のようなので、公式サイトから「1.0.2p」を落としてコンパイル。
% openssl version OpenSSL 1.0.2p 14 Aug 2018
以下のサイトの「libevent-client.c」を参考にコードを追加する。
Tutorial: HTTP/2 client — nghttp2 1.33.0-DEV documentation
SSL_CTX_set_alpn_protos(ctx, (const unsigned char *)"\x02h2", 3); SSL_set_alpn_protos(ssl, (const unsigned char *)"\x02h2", 3);
これでリクエストを送信する準備が整った。
続いて、SSL_write()でサーバへ渡している内容を置き換える(frameと呼ばれるバイナリ形式のフォーマットを使う)
http2 最速実装 v2
今回はここまで。


