パラメータ推定(混合正規分布)
混合分布を使うことで、より柔軟に分布をモデル化できる。
例えば、ピークが2つあるような分布。
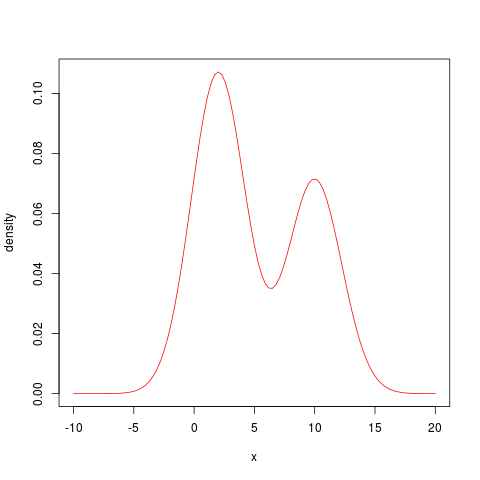
これは以下2つの分布を混合したもの。
分布1 : 正規分布N(2, 5)、混合比「0.6」
分布2 : 正規分布N(10, 5)、混合比「0.4」
この混合分布は音声認識において使われていて、隠れマルコフモデル(HMM)の各状態の出力確率が混合正規分布(混合ガウス分布)に従うとしたモデルを「GMM-HMM」と呼ぶ。
具体的にどのようにモデル化しているかは以下の記事に書いた。
work-in-progress.hatenablog.com
混合数をKとおく。
混合パラメータ
観測データがN個のときの対数尤度関数
xが与えられたとき、それに対応する確率密度を各分布ごとに分解した割合を仮置きするために、潜在変数zを導入する。
潜在変数zは、K個の要素からなり、どれか1つだけ1を取り、他は全て0となる。
xについてn番目の値が与えられたとき、k番目のzが1となる確率を負担率と呼び、以下の式で計算する。
分母は、混合分布における、n番目のxの確率密度。
分子は、k番目の分布における、n番目のxの確率密度となるので、負担率は
この辺は以下のサイトを参考にさせていただいた。
混合ガウスモデルとEM - 人工知能に関する断創録
負担率はN個のxのそれぞれについて求まる。
この負担率を使って、パラメータ(平均、分散、混合比)の最尤値を計算する。
負担率を求めるためにはパラメータが必要で、パラメータの最尤値を計算するためには負担率が必要と、循環してしまうので、以下の2ステップに分けて計算する。
- Eステップ:現在の混合比、平均、分散に対応する負担率を計算する
- Mステップ:Eステップで計算した負担率をもとに、混合比、平均、分散の最尤値を求める
混合ガウス分布の数が「2」、各分布が以下であるサンプルデータ「500」個用意し、推定の過程を追ってみる。
分布1 : 正規分布、平均「2」、分散「5」、混合比「0.6」
分布2 : 正規分布、平均「10」、分散「5」、混合比「0.4」
rnorm関数に与えるseedは「123」を指定。
[1] 0.7467384 1.4853075 5.4853777 2.1576616 2.2890962 9.7872438 [7] 3.0306400 -0.8287629 0.4641503 1.0034695 9.7822757 2.8045682 [13] 2.8961522 10.4597300 8.6216076 5.9956592 9.7052800 -2.3974896 (snip) [486] 3.741583972 4.045495218 11.760084269 5.637816986 13.701085639 [491] 11.511050698 5.139551842 4.893659583 9.523030728 10.700400827 [496] 9.798809343 12.393746629 2.368595386 8.831393539 3.234662183
密度プロット(赤い線はcurve関数で書いた真の確率密度関数)
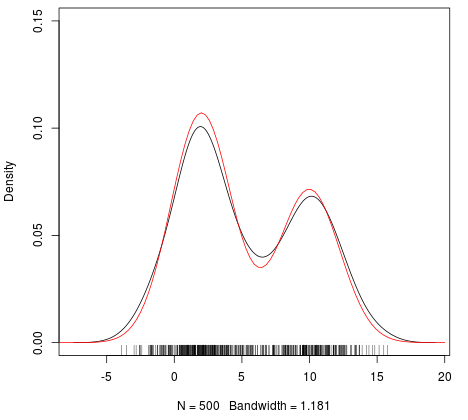
「R」には「mixtool」ライブラリで「normalmixEM」関数が用意されているので、これを使えば最尤値を求められる。
検算の意味で最初に値を求めておく。
mixtool_val <- normalmixEM(data, k=2)
最尤値での対数尤度
mixtool_val$all.loglik[length(mixtool_val$all.loglik)] -1388.84
最尤値(混合比、平均、分散)
mixtool_val$lambda [1] 0.589741 0.410259 # 混合比 mixtool_val$mu [1] 1.969816 10.129432 # 平均 mixtool_val$sigma^2 [1] 4.498699 4.566088 # 分散
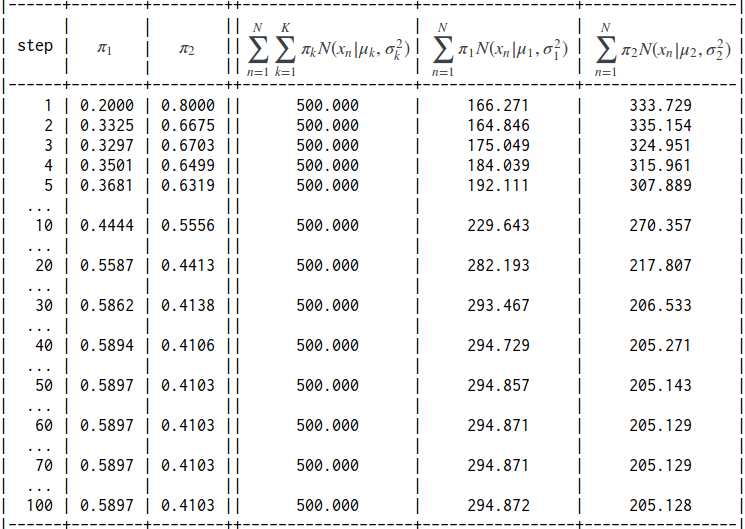
先ほどの式で最尤値を100回、計算してみた結果。
初期値は、以下の値を与えた。
分布1 : 混合比0.2、平均1、分散2
分布2 : 混合比0.8、平均5、分散2

負担率の推移。
パラメータ推定(ニュートン・ラフソン法)
前回の続き。
「ニュートン・ラフソン法」を使って、2変数パラメータの最尤推定値を求めてみる。
以下のサイトを参考にさせていただいた。
http://www012.upp.so-net.ne.jp/doi/sas/numerical/Newton_Raphson/Newton_Raphson.pdf
正規分布の対数尤度関数を再掲。
データ
# 平均2、分散5の正規分布に従うサンプルを200個 set.seed(123); data <- rnorm(200, mean=2, sd=sqrt(5)) [1] 0.746738355 1.485307487 5.485377748 2.157661556 2.289096164 [6] 5.835001897 3.030639969 -0.828762916 0.464150333 1.003469540 [11] 4.737130109 2.804568177 2.896152207 2.247494077 0.757101438 (snip) [186] 1.559101297 4.481857217 2.189478346 3.686115522 0.883549109 [191] 2.479514290 1.273980231 2.211495199 -0.002093333 -0.931041334 [196] 6.465904894 3.343225764 -0.797927823 0.633391465 -0.650814055
初期パラメータは、平均1、分散1とおいて、先ほどの式を計算した結果。

最尤値となるパラメータは、平均「1.980836」、分散「4.425514」
検算。Rの関数で計算した結果。
# 準ニュートン法による最適解 > optim(c(1, 1), fn=log_likelihood_norm, obs=data, method="BFGS", control=list(fnscale=-1), hessian=TRUE)
結果
$par [1] 1.980839 4.425508 $value [1] -432.5263 $counts function gradient 31 10 $convergence [1] 0 $message NULL $hessian [,1] [,2] [1,] -4.519255e+01 3.119993e-05 [2,] 3.119993e-05 -5.105931e+00
小数点第五位まで一致していることが確認できた。
また、k回目の最尤値でのヘッセ行列を固有値分解してみる。
H_0 <- matrix(c(-200.000000 , -196.167181 , -196.167181 , -977.510617 ), nrow=2) H_1 <- matrix(c(-152.232794 , -35.661895 , -35.661895 , -340.743870 ), nrow=2) H_2 <- matrix(c(-108.715893 , -7.280127 , -7.280127 , -113.101423 ), nrow=2) H_3 <- matrix(c( -79.549506 , -1.429134 , -1.429134 , -39.900363 ), nrow=2) H_4 <- matrix(c( -61.130669 , -0.254284 , -0.254284 , -15.933080 ), nrow=2) H_5 <- matrix(c( -50.656386 , -0.036104 , -0.036104 , -7.966423 ), nrow=2) H_6 <- matrix(c( -46.162098 , -0.002919 , -0.002919 , -5.555946 ), nrow=2) H_7 <- matrix(c( -45.231581 , -0.000058 , -0.000058 , -5.123588 ), nrow=2) H_8 <- matrix(c( -45.192558 , -0.000000 , -0.000000 , -5.105933 ), nrow=2) H_9 <- matrix(c( -45.192490 , -0.000000 , -0.000000 , -5.105903 ), nrow=2)
固有値分解の結果

最尤値をとるパラメータを与えたとき、ヘッセ行列の固有ベクトルは標準基底になっている。
また、各パラメータの2階偏微分の値が固有値になっている。
推定するパラメータが2つの場合、フィッシャー情報行列は以下として定義される。
今回は1セットのデータのみ用いており、パラメータ推定値も1セットのみであるから、フィッシャー情報行列は、対数尤度関数の2階偏微分にマイナスを掛けたものになる。
今回、各繰り返しにおけるフィッシャー情報量と対数尤度は以下のとおりであった。

平均を固定して、分散を変えてみると以下のとおりであった。

フィッシャー情報行列は、対数尤度関数のスコア関数(1階偏微分)の分散として定義されるから、以下のことがいえる。
- スコア関数の分散が大きい(=フィッシャー情報量が大きい)ほど、相対的に尤度は下がる
- スコア関数の分散が小さい(=フィッシャー情報量が小さい)ほど、相対的に尤度は上がる
パラメータ推定(最尤推定法)
今、手元にn個の観測値(標本)が得られているとする。
統計モデルとして表現するには、
が必要となる。
1番目の確率分布の形が分かったとして、2番目のパラメータを推定する方法の1つである「最尤推定法」に関するメモ。
ある1つの観測値が、他の観測値に影響を及ぼさない(確率変数は独立している、という)場合、それぞれの観測値の確率密度を掛けあわせたもの(同時確率)が尤度関数となる。
観測値つまり確率変数をx、未知パラメータをθとおくと、尤度関数は以下の形で表される。
\[
L(\theta) = \displaystyle \prod_{ i = 1 }^n f(x_i | \theta)
\]
尤度関数すなわち同時確率を最大にするパラメータθの値が「最尤推定値」になる。
小数の乗算はアンダーフローを引き起こすので、尤度関数の対数をとった「対数尤度関数」を最大化するパラメータθを求める。
具体的に見てみる。
確率分布の形が「正規分布」だとすると、推定したいパラメータθ は、
となる。
(μは平均、σは標準偏差を表す)
を対数尤度関数の式にあてはめて、式変形する。
導出過程は以下のサイトを参照。
統計学的画像再構成法である
これをRの関数として定義する。
第1項は定数なので、最大化を考えるにあたっては無視できるが、今回は確認用に残しておく。
対数尤度関数(正規分布)
# arg1 : vector(size 2), [1]mean, [2]variance # arg2 : vector(size N), observation log_likelihood_norm <- function(param, obs){ mu <- param[1]; sigma2 <- param[2]; term1 <- (-1) * length(obs) * 0.5 * log(2*pi) term2 <- (-1) * length(obs) * 0.5 * log(sigma2); term3 <- (-1) * 0.5 / sigma2 * sum((obs-mu)^2); return ( term1 + term2 + term3 ); }
検算。
平均「2」、分散「5」の正規分布に従う乱数を10個用意する。
> data <- rnorm(10, mean=2, sd=sqrt(5)) > data [1] -0.01731340 1.79861872 2.99598784 1.78515021 2.42412228 -1.61575147 [7] 1.74058535 3.84369888 1.93563703 0.03983286
Rのdnorm関数を使って求めた結果
value <- 0 for (i in 1:length(data)) { value <- value + log(dnorm(data[i], mean=2, sd=sqrt(5))) } value # -19.80805 value <- 1 for (i in 1:length(data)) { value <- value * dnorm(data[i], mean=2, sd=sqrt(5)) } log(value) # -19.80805
作成した関数での結果
log_likelihood_norm(c(2, 5), data) # -19.80805
一致していることを確認。
値が最大になるパラメータをRのoptim関数を使って探してみる。
最適解(サンプル数10)
optim(c(0.5, 1), fn=log_likelihood_norm, obs=data, control=list(fnscale=-1), hessian=FALSE) # $par # [1] 1.493105 2.313280 # $value # [1] -18.38531 # $counts # function gradient 73 NA # $convergence # [1] 0
出てきた最適値は、平均が「1.493105」、分散が「2.313280」
統計量(サンプル数10)
mean(data) # [1] 1.493057 # 不偏分散 var(data) # [1] 2.571645 # 標本分散 variance <- function(x) { var(x) * (length(x)-1) / length(x) } variance(data) # [1] 2.31448
サンプル数を100に増やしてみる。
最適解(サンプル数100)
data <- rnorm(100, mean=2, sd=sqrt(5)) optim(c(0.5, 1), fn=log_likelihood_norm, obs=data, control=list(fnscale=-1), hessian=FALSE) # $par # [1] 1.918190 4.851344 # $value # [1] -220.8375 # $counts # function gradient 59 NA # $convergence # [1] 0
出てきた最適値は、平均が「1.918190」、分散が「4.851344」
統計量(サンプル数100)
mean(data) # [1] 1.917897 var(data) # [1] 4.898471 variance(data) # [1] 4.849486
さらにサンプル数を増やしてみる。
最適解(サンプル数1000)
data <- rnorm(1000, mean=2, sd=sqrt(5)) optim(c(0.5, 1), fn=log_likelihood_norm, obs=data, control=list(fnscale=-1), hessian=FALSE) # $par # [1] 1.891001 4.752660 # $value # [1] -2198.32 # $counts # function gradient 63 NA # $convergence # [1] 0
統計量(サンプル数1000)
mean(data) # [1] 1.891252 var(data) # [1] 4.7577 variance(data) # [1] 4.752943
サンプル数が多くなるほど、標本分散と不偏分散の差が少なくなっている。
対数尤度関数が返す値の3次元散布図を書いてみる。
meanが「2の前後3、-1から5まで1刻みの7通り」、sigma2は「5の前後3、2から8まで1刻みの7通り」の49パターンとした。

一番高くなるところのパラメータが最尤推定値となる。
最尤推定値を求めるにあたって、Rのoptim関数では以下の最適化アルゴリズムが使える模様。
method="Nelder-Mead" # シンプレックス法、関数が微分できなくても可 method="BFGS" # 準ニュートン法 method="L-BFGS-B" # 準ニュートン法の変種(推定するパラメータのlower/upperを指定) method="CG" # 共役勾配法 method="SANN" # シミュレーテッド・アニーリング法、関数が微分できなくても可
methodパラメータの省略時デフォルトは「Nelder-Mead」(シンプレックス法)
optim function | R Documentation
The default method is an implementation of that of Nelder and Mead (1965), that uses only function values and is robust but relatively slow.
It will work reasonably well for non-differentiable functions.
(参考)多変量正規分布のパラメータ推定で、optim関数のmethodを変えて比較してみた結果
パラメータ推定(多変量正規分布) - ichou1のブログ
ヘッセ行列の固有値による凸性の判定
最適化を考える時、どの方向に向かって修正していくかを決める必要がある。
扱う対象が関数化できるなら、その最大値(あるいは最小値)を求める問題に帰着するので、関数の凸性が大事な概念になってくる。
今回は2変数関数を対象に、2階偏微分であるヘッセ行列を使って凸性を調べる方法を見てみる。
以下のサイトを参考にさせていただいた。
http://www2.kaiyodai.ac.jp/~yoshi-s/Lectures/Optimization/2013/lecture_1.pdf
偏微分の順番で微分結果は変わらないので、ヘッセ行列は対称行列になる。
3パターンの関数で見てみる。
[パターン1] 狭義凸関数
ヘッセ行列が正定値(固有値が全て0より大きい)
グラフが全ての方向で丸く突き出ている
[パターン2] 凸関数(狭義凸関数ではない)
ヘッセ行列が半正定値(固有値が全て0以上)
2点を結ぶ線分とグラフが重なる部分がある
勾配ベクトル
ヘッセ行列
ヘッセ行列を固有値分解する。
固有値は「2」であることを確認
> eigen(matrix(c(2, 0, 0, 2), nrow=2, ncol=2, byrow=TRUE))
eigen() decomposition
$values
[1] 2 2
$vectors
[,1] [,2]
[1,] 0 -1
[2,] 1 0角度を変えてみる
y軸が奥行きと重なるように見たところ

x軸が奥行きと重なるように見たところ

全ての方向で丸く突き出た形をしている。
[パターン2] 凸関数(狭義凸関数ではない)

勾配ベクトル
ヘッセ行列
ヘッセ行列を固有値分解する。
固有値は「2」と「0」であることを確認
> eigen(matrix(c(0, 0, 0, 2), nrow=2, ncol=2, byrow=TRUE))
eigen() decomposition
$values
[1] 2 0
$vectors
[,1] [,2]
[1,] 0 -1
[2,] 1 0角度を変えてみる。
y軸が奥行きと重なるように見たところ
グラフの底が、線分の形をしている。

x軸が奥行きと重なるように見たところ

[パターン3] 凸面と凹面が混在する関数

勾配ベクトル
行列の低ランク近似と近似度
特異値分解を使った「行列の低ランク近似」に関するメモ。
まずは、視覚的に確認しやすい画像データで試してみる。
高さ200px、幅320px、インデックスカラーのRAWデータを用意する。

1pxを1バイトで表現、0〜255の範囲の値をとる200行 x 320列の行列ができる。
以下は左上を拡大した画像。
先頭6バイト分のみ値を添えてみた。値が小さいほど黒に近く、値が大きいほど白に近くなる。

CSVに落としたものをRに読み込み、
A <- data.matrix(read.table("200_320_gray_scale.csv", header=F, sep=","))
ランク数を「r」とおいて、特異値分解する。
A.svd <- svd(A) u <- A.svd$u[,1:r, drop=F] d <- diag(A.svdA$d)[1:r, 1:r, drop=F] v <- A.svd$v[,1:r, drop=F]
そして、再度、csvに書き戻す。
write.table(round(u %*% d %*% t(v)), str_c("200_320_gray_scale_low_rank_approximate_", r), ".csv"), sep=",", row.names=FALSE, col.names=FALSE)
r = 1

r = 1 (拡大)

r = 10

r = 10 (拡大)

r = 20

フロベニウスノルム(元々の行列)
norm(A, "F") # 26607.34
続けて、近似した行列のフロベニウスノルム
フロベニウスノルム(ランク1、5、10、15、20、25、50、75、100で近似した行列)
norm(A_rank1, "F") # 25696.45 norm(A_rank5, "F") # 26186.34 norm(A_rank10, "F") # 26333.71 norm(A_rank15, "F") # 26412.39 norm(A_rank20, "F") # 26460.39 norm(A_rank25, "F") # 26493.76 norm(A_rank50, "F") # 26570.16 norm(A_rank75, "F") # 26594.95 norm(A_rank100, "F") # 26603.22
近似に使うランク数を大きくするほど、フロベニウスノルムも大きくなっていることが確認できる。
尚、特異値の上位20は以下のとおりであった。
> A.svd$d[1:20] [1] 25695.8853 3754.6842 2374.1272 1782.2953 1588.0870 1466.8724 [7] 1308.7928 1248.0294 1112.3381 1042.8967 983.9771 963.9730 [13] 916.1656 841.3105 837.3214 794.9816 735.2430 722.9311 [19] 685.1815 634.1618
下位20は以下のとおり。
> A.svd$d[180:200] [1] 15.898742 15.417982 14.987853 14.435300 14.174012 13.721447 13.289164 [8] 12.747505 12.436280 11.677728 11.473563 11.297093 10.792612 10.623457 [15] 9.714841 9.523776 9.005887 8.843195 8.200154 8.091183 7.484766
各ランクの特異値(ランク1〜200)

各ランクの特異値(ランク11〜200)

(参考)特異値を全部足すと以下のとおり。
> sum(A.svd$d) [1] 75484.84
音声認識メモ(Kaldi)その26(パラメータ更新、NG-SGD Dan's DNN(nnet2))
パラメータ更新の過程でやっていることは「Natural Gradient for Stochastic Gradient Descent (NG-SGD)」と名前が付いている。
用語のおさらい。
「Stochastic Gradient Descent」(確率的勾配降下法)は、シャッフルした訓練データで勾配を計算、パラメータ更新を繰り返す反復法。1つの訓練データを使うのがオンライン学習、複数の訓練データを使うのがミニバッチ学習。
「Natural Gradient method」は、彼らの研究での用語で、フィッシャー情報量行列の逆行列(近似)を学習率行列として使う方法とある。
previous work has used the term “Natural Gradient” to describe methods like ours which use an approximated inverse-Fisher matrix as the learning rate matrix, so we follow their precedent in calling our method “Natural Gradient”.
コアとなる計算は、N行からなる行列Xがあったとして、i番目の行ベクトル「x_i」にフィッシャー情報量(F_i)の逆数を掛ける。

ここでのフィッシャー情報量「F_i」は、i番目の行を除く他の行「x_ j」から求める。

この考え方をベースに、以下2つの拡張を加えたとある。
- smoothing of F_i with the identity matrix (単位行列によるF_iの平滑化)
- scaling the output to have the same Frobenius norm as the input(入力と同じフロベニウスノルムを持つよう出力をスケール)
ここで、N行 x D列の行列「X_t」があるとし、「X_t」をcolumn-wise(列方向)で考えると、フィッシャー情報量行列「F_i」はD行xD列になる(X^T X)
フィッシャー情報量行列をR次元で低ランク近似して、

t : ミニバッチindex
F_t : D行 x D列
R_t : R行 x D行
D_t : R行 x R行
I : D行 x D列、identity matrix(単位行列)
rho_t : 0 < rho_t
逆行列(近似したもの)を求める。


G_t : D行 x D列
E_t : R行 x R行
beta_t : scalar
column-wise(列方向)なので、乗算は「X_t」の右側から掛けて「X_t」を更新する。

この部分は前回の以下部分にあたる。

続けてスケーリング。

この部分は前回の「gamma_t」にあたる。

細かく見てみる。
更新対象であるパラメータの次元(D)が「376」、ミニバッチサイズ(N)が「128」、低ランク近似の次元(R)が「30」であるとする。
行列X_t(N行 x D列)は、転置行列を掛けあわせて対称行列にした上で計算する。
尚、論文上では、
パラメータの次元(D) < ミニバッチの次元(N)
を想定してcolumn-wise(列方向)になっている。
(学習が進むにつれて、ミニバッチサイズは大きくなっていく(例えば「512」))
計算はD次元(=full-rank)の対称行列「T_t」(D行 x D列)に対してではなく、

S_t : D行 x D列

eta : forgetting factor、0 < η < 1
R次元(=row-rank approximation)の対称行列「Z_t」(R行 x R列)に対して行う。

Y_t : R行 x D列
R_t : R行 x D行
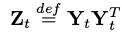
上記の「R_t」をスケールしたものを「W_t」と置き、

W_t : R行 x D行
これを重み行列として適正値に更新することがターゲットとなる。
まずは「R_t」を初期化する。
これはR次元の直交行列を横に並べた形になる。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::InitDefault()
// after the next line, W_t_ will store the orthogonal matrix R_t. InitOrthonormalSpecial(&W_t_);
R_t (R x D)

「E_t」の初期値を求め、その0.5乗(平方根)を掛ける。
BaseFloat E_tii = 1.0 / ( 2.0 + (D + rank_) * alpha_ / D );
// W_t =(def) E_t^{0.5} R_t.
W_t_.Scale(sqrt(E_tii));次のミニバッチに向けて「W_t」を更新する。
更新式は以下のとおり。

W_t1 : R行 x D列
E_t1 : R行 x R行、diagonal matrix(対角行列)
R_t1 : R行 x D列
C_t : R行 x R行、diagonal matrix(対角行列)
U_t : R行 x R列、Orthogonal matrix(直交行列)
Y_t : R行 x D列
J_t : R行 x D列
D_t : R行 x R行
eta : forgetting factor、0 < η < 1
「U_t」(直交行列)と「C_t」(特異値)は、「Z_t」を特異値分解して得られる。

以下、「Z_t」を求める過程。
元々のインプット「X_t」(N行 x D列)に、「W_t」(R行 x D列)の転置行列を右から掛けて、「H_t」(N行 x R列)を求める(「N」はミニバッチサイズ)
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
H_t.AddMatMat(1.0, *X_t, kNoTrans, W_t, kTrans, 0.0); // H_t = X_t W_t^T
H_t (N x R)

列数「D」(376次元)のインプット(X_t)が、列数「R」(30次元)の行列になる。
続けて、「J_t」を求める。
元々のインプット「X_t」(N行 x D列)に「H_t」(N行 x R列)の転置行列を左から掛け合わせて「J_t」(R行 x D列)を求める。
(「W_t」と同じ行数、列数になる)
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
J_t.AddMatMat(1.0, H_t, kTrans, *X_t, kNoTrans, 0.0); // J_t = H_t^T X_t
「J_t」を式変形すると
J_t = H_t^T X_t
= (X_t W_t^T)^T X_t
= W_t X_t^T X_t「X_t」(N行 x D列)の「uncentered covariance matrix」(D行 x D列)に、Weight Matrix(R行 x D列)を左から掛けたものとも言える。
J_t (R x D)

続けて「K_t」を求める。
「J_t」(R行 x D列)に対し、転置行列を右から掛けたものにあたる。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
K_t.SymAddMat2(1.0, J_t, kNoTrans, 0.0); // K_t = J_t J_t^T
K_t (R x R、symmetric)

続けて「L_t」を求める。
「H_t」(N行 x R列)に対し、転置行列を左から掛けたものにあたる。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
L_t.SymAddMat2(1.0, H_t, kTrans, 0.0); // L_t = H_t^T H_t
L_t (R x R、symmetric)

「K_t」と「L_t」を使って、「Z_t」を求める。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
SpMatrix<double> Z_t_double(R); ComputeZt(N, rho_t, d_t, inv_sqrt_e_t, K_t_cpu, L_t_cpu, &Z_t_double);
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
Matrix<BaseFloat> U_t(R, R); Vector<BaseFloat> c_t(R); // do the symmetric eigenvalue decomposition Z_t = U_t C_t U_t^T. Z_t_scaled.Eig(&c_t, &U_t); SortSvd(&c_t, &U_t); c_t.Scale(z_t_scale);
C_t (30次元)
0.957 0.164 0.119 0.090 ... 0.00019 0.00016
U_t (R x R)

「W_t」を更新する。

[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
CuMatrix<BaseFloat> W_t1(R, D); // W_{t+1}
ComputeWt1(N,
d_t,
d_t1,
rho_t,
rho_t1,
U_t,
sqrt_c_t,
inv_sqrt_e_t,
W_t,
&J_t,
&W_t1);「B_t」を求める。
B_t (R x D)

[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::ComputeWt1()
// B_t = J_t + (1-eta)/(eta/N) (D_t + rho_t I) W_t J_t->AddDiagVecMat(1.0, w_t_coeff_gpu, W_t, kNoTrans, 1.0);
w_t_coeff_gpu : R行 x R行、対角行列、W_tの各行に対する係数
式変形すると以下のとおり。
B_t = J_t + ( W_t係数 * W_t )
= ( W_t X_t^T X_t ) + ( W_t係数 * W_t )「A_t」を求める。
A_t (R x R)

[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::ComputeWt1()
// A_t = (eta/N) E_{t+1}^{0.5} C_t^{-0.5} U_t^T E_t^{-0.5} B_t
Matrix<BaseFloat> A_t(U_t, kTrans);
for (int32 i = 0; i < R; i++) {
BaseFloat i_factor = (eta / N) * sqrt_e_t1(i) * inv_sqrt_c_t(i);
for (int32 j = 0; j < R; j++) {
BaseFloat j_factor = inv_sqrt_e_t(j);
A_t(i, j) *= i_factor * j_factor;
}
}「W_t1」を求める。
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::ComputeWt1()
// W_{t+1} = A_t B_t
CuMatrix<BaseFloat> A_t_gpu(A_t);
W_t1->AddMatMat(1.0, A_t_gpu, kNoTrans, *J_t, kNoTrans, 0.0);「W_t1」を使って「X_t」を更新する。

これを繰り返して、更新された「X_t」が、前回見た「in_value_temp」、「out_deriv_temp」に該当する。
[ nnet2/nnet-component.cc ] AffineComponentPreconditionedOnline::Update()
preconditioner_in_.PreconditionDirections(&in_value_temp,
&in_row_products,
&in_scale);
preconditioner_out_.PreconditionDirections(&out_deriv_temp,
&out_row_products,
&out_scale);パラメータの修正ベクトルとして使い、モデルのパラメータを更新。
[ nnet2/nnet-component.cc ] AffineComponentPreconditionedOnline::Update()
bias_params_.AddMatVec(local_lrate, out_deriv_temp, kTrans, precon_ones, 1.0); linear_params_.AddMatMat(local_lrate, out_deriv_temp, kTrans, in_value_precon_part, kNoTrans, 1.0);
固有値分解と座標変換
DNN(Deep Neural Network)を学んでいると、擬似逆行列の算出や低ランク近似などで固有値の概念に出くわす。
固有値分解に関するメモ。
以下のサイトを参考にさせていただいた。
http://eman-physics.net/math/linear09.html
変換に使う行列Aは参考サイトと同じもの使用。
固有値
D <- diag(A.eigen$values) [,1] [,2] [1,] 5 0 [2,] 0 2
固有ベクトル
# 固有値5に属する固有ベクトル(正規化)) U1 <- A.eigen$vectors[,1] [1] -0.4472136 -0.8944272 # 固有値2に属する固有ベクトル(正規化)) U2 <- A.eigen$vectors[,2] [1] -0.7071068 0.7071068
2つのベクトルの内積は非ゼロなので、
# 2つの固有ベクトルの内積 U1 %*% U2 [,1] [1,] -0.3162278
2つの固有ベクトル( -0.45, -0.89 )、 ( -0.71, 0.71 )は直交しない。
視覚化してみる。
適当な4つの点P1( 1, 2 )、P2( 1, 1 )、P3( 1, 0 )、P4( -1, -2 )を選ぶ。
P1 <- matrix(c(1, 2), nrow=2, ncol=1, byrow=FALSE) P2 <- matrix(c(1, 1), nrow=2, ncol=1, byrow=FALSE) P3 <- matrix(c(1, 0), nrow=2, ncol=1, byrow=FALSE) P4 <- matrix(c(-1, -2), nrow=2, ncol=1, byrow=FALSE)

1次変換によって移される座標を求める。
P1の1次変換
A %*% P1 [,1] [1,] 5 [2,] 10
(1, 2)から(5, 10)へ移った。
P2の1次変換
A %*% P2 [,1] [1,] 4 [2,] 6
(1, 1)から(4, 6)へ移った。
P3の1次変換
A %*% P3 [,1] [1,] 3 [2,] 2
(1, 0)から(3, 2)へ移った。
P4の1次変換
A %*% P4 [,1] [1,] -5 [2,] -10
(-1, -2)から(-5, -10)へ移った。
変換前と変換後の座標をプロットしてみる。
白抜きが元の座標、同じ形の黒塗りが1次変換によって移された座標を示す。

ここでは、P1とP4が該当。
P1に関しては(1, 2)だったものが(5, 10)に移っており、5倍(固有値と同じ)されている。
また、P4に関しては(-1, -2)だったものが(-5, -10)に移っており、同じく5倍(固有値と同じ)されている。
固有ベクトルを基底とする新しい座標軸で、各点がどう表現されるか確認。
固有ベクトルを列ベクトルとして表し、横に並べた行列
V <- A.eigen$vectors [,1] [,2] [1,] -0.4472136 -0.7071068 [2,] -0.8944272 0.7071068
この逆行列を、元の座標を表す列ベクトルの左から掛けることで、新しい基底での座標が求まる。
何故こんなことをするのかは、無相関化の項をご参照。
work-in-progress.hatenablog.com
P1の新座標表現
solve(V) %*% P1 [,1] [1,] -2.236068e+00 [2,] 2.220446e-16
小数点第二位を四捨五入すると(-2.24, 0)
P2の新座標表現
solve(V) %*% P2 [,1] [1,] -1.4907120 [2,] -0.4714045
小数点第二位を四捨五入すると(-1.49, -0.47)
P3の新座標表現
solve(V) %*% P3 [,1] [1,] -0.745356 [2,] -0.942809
小数点第二位を四捨五入すると(-0.75, -0.94)
P4の新座標表現
solve(V) %*% P4 [,1] [1,] 2.236068e+00 [2,] -2.220446e-16
小数点第二位を四捨五入すると(2.24, 0)
プロットしてみる。
元々の基底(1, 0)、(0, 1)は消して、新しい基底(-0.45, -0.89)、 (-0.71, 0.71)を描画。
枠外の目盛りは元々の基底(1, 0)、(0, 1)のもの。目印として残した。

拡大。

座標軸の正負の向きが標準基底と同じになるよう、回転および反転。

再掲
P1(-2.24, 0) <== 標準基底での表現(1, 2)
P2(-1.49, -0.47) <==標準基底での表現(1, 1)
P3(-0.75, -0.94) <==標準基底での表現(1, 0)
P4(2.24, 0) <==標準基底での表現(-1, -2)







